Explaining Empowerment.
Reinforcement Learning is hard. Despite the various successes of Deep Reinforcement Learning, a limitation of the standard reinforcement learning approach is that an agent is only able to learn using external rewards obtained from it’s environment. Truly autonomous agents are required to function in environments with no rewards or very sparse reward signals.
Intrinsically motivated reinforcement learning is a variant that aims to tackle the problem of no reward reinforcement learning by equipping the agent with intrinsic rewards such as Curiosity (Curiosity is all you need) and Empowerment (There could be many other formulations).
What all these definitions/formulations have in common is the way they allow an agent to reason about the value of information in the action-state sequences it observes.
Empowerment is one such measure that which is defined as the channel capacity (Information theory reference ) between actions and states that maximizes the influence of an agent on it’s near future.
Information theoretically, empowerment is defined as the mutual information between the action and the subsequent state acheived by that action. Policies that take into account the empowerment of a state consistently drives the agent to states with high potential. Empowerment basically alows the agent to take only those actions which result in the maximum possible number of future states. Empowerment improves survival.
This all sounds fine and dandy. Then why don’t we see much of empowerment in the current literature. Because it is seriously hard to calculate the empowerment. Really hard.
It requires the calculation of Mutual information which has been , traditionally, a very hard quantity to calculate. Moreover, the current literature on using empowerment tend to have complicated architectures and often do not have great performance, especially on hard exploration games.
What are the solutions ?
Variational Empowerment: There are varying methods to calculate these which are kind of similar and just vary in the way how the lower bound to the mutual information is calculated.
What is mutual information ?
Mutual information is a quantity that is used for measuring the relationship between random variables. It is defined as the decrease in uncertanity of a random variable x given another random variable z. This means that if you have now something about z then you are more confident about x.
Why use mutual information and not correlation?
Mutual information, unlike correlation, is able to capture non-linear statistical dependencies between random variables.
KL Divergence Representation
What is the KL Divergence ? - The KL Divergence measures how one probability distribution p diverges from a second expected probability distribution q.
MI is equivalent to the KL divergence between the joint and the product of the marginals. Larger the divergence, stronger the interdependence between the random variables. Note that MI can also be represented in the form of the shannon entropies.
What is empowerment ? Mathematically.
Empowerment is defined as the mutual information between the control input and the subsequent state.
where w is the source distribution policy (Not to be confused with the empowerment(or intrinsic reward) maximizing policy). Note that we could also use the empowerment maximizing policy as the action policy.
Empowerment KL Divergence Representation
Empowerment can be represented in the KL divergence because MI has a KL divergence representation.
The marginal transition p(s’|s) is the problem here. For continuous action spaces especially. Since we need to integrate over all actions to get this probability distribution. (Note, later in the post we will look at empowerment for discrete action spaces).
Two Ways to circumvent this intractable distribution:
1.Approximate p(s’|s) using variational approximation. (Non-trivial) 2.Replace p(s’|s) with the planning distribution (inverse dynamics distribution), p(a|s’, s) and approximate this (still intractable) distribution. (Much easier than 1).
How do we use the planning distribution?
Avoid the integral over all actions by switching to the planning distribution.
Despite being intractable, the planning distribution can be approximated by another distribution q(a|s’, s). So finally we have the lower bound to the mutual information that we required.
Since, I is constant with respect to q, maximizing the lower bound with respect to the planning distribution approximation (q) and the source distribution w, we can maximze the mutual information (or empowerment).
One caveat: This lower bound is dependent on how well the distribution q is able to approximate the true planning distribution. Better the approximation, tighter the lower bound.
How do we calculate the lower bound ?
We can sample from the system dynamics (assuming it is available) and the source distribution and estimate the gradients of the lower bound of Mutual Information using Monte Carlo Sampling and the reparameterization trick. (Simple explanation of the reparameterization trick) The following method is essentially the method demonstrated in Unsupervised Real-time control through Variational Empowerment.
Exploiting the reward (or the Empowerment)
The estimation of the empowerment enables us to efficiently learn the source distribution, w. The main goal of this training is not to lean a policy but to learn to estimate empowerment of a particular state. Empowerment can be perceived as the unsupervised value of a state, it can be used to train agents that proceed towards empowering states. The reward in the reinforcement learning setting is then the negative empowerment value.
Enough of maths. Practical Approach.
Have 3 networks-
- Forward Dynamics Model that takes in the current state and the action and predicts the next state.
- The Policy Network, pi, that takes in the current state and predicts the action.
- The Source network, w, that takes in the current state and predicts the action (this is used for the calculation of the empowerment of a state).
- The Planning Network, q, that takes in the current and the next state and predicts the action (this is similar to the inverse dynamics model in Curiosity is all you need)
The Training Loop:
- Sample the environment using the Policy Network.
- Train the forward dynamics model.
- Sample one step action from the source distribution and the next state from the forward dynamics model.
- Calculate the mutual information (the Empowerment).
- Calculate the reward function. (A function of the Empowerment)
- Gradient ascent on w and q.
- Gradient ascent on pi.
Network Architectures
States Encoder (Better results when using state encodings instead of raw observations)
class Encoder(nn.Module):
def __init__(self,
state_space,
conv_kernel_size,
conv_layers,
hidden,
input_channels,
height,
width
):
super(Encoder, self).__init__()
self.conv_layers = conv_layers
self.conv_kernel_size = conv_kernel_size
self.hidden = hidden
self.state_space = state_space
self.input_channels = input_channels
self.height = height
self.width = width
# Random Encoder Architecture
self.conv1 = nn.Conv2d(in_channels=self.input_channels,
out_channels=self.conv_layers,
kernel_size=self.conv_kernel_size, stride=2)
self.conv2 = nn.Conv2d(in_channels=self.conv_layers,
out_channels=self.conv_layers,
kernel_size=self.conv_kernel_size, stride=2)
self.conv3 = nn.Conv2d(in_channels=self.conv_layers,
out_channels=self.conv_layers * 2,
kernel_size=self.conv_kernel_size, stride=2)
self.conv4 = nn.Conv2d(in_channels=self.conv_layers * 2,
out_channels=self.conv_layers * 2,
kernel_size=self.conv_kernel_size, stride=2)
# Leaky relu activation
self.lrelu = nn.LeakyReLU(inplace=True)
# Hidden Layers
self.hidden_1 = nn.Linear(in_features=self.height // 16 * self.width // 16 * self.conv_layers * 2,
out_features=self.hidden)
self.output = nn.Linear(in_features=self.hidden, out_features=self.state_space)
# Initialize the weights of the network (Since this is a random encoder, these weights will
# remain static during the training of other networks).
nn.init.xavier_uniform_(self.conv1.weight)
nn.init.xavier_uniform_(self.conv2.weight)
nn.init.xavier_uniform_(self.conv3.weight)
nn.init.xavier_uniform_(self.conv4.weight)
nn.init.xavier_uniform_(self.hidden_1.weight)
nn.init.xavier_uniform_(self.output.weight)
def forward(self, state):
x = self.conv1(state)
x = self.lrelu(x)
x = self.conv2(x)
x = self.lrelu(x)
x = self.conv3(x)
x = self.lrelu(x)
x = self.conv4(x)
x = self.lrelu(x)
x = self.hidden_1(x)
x = self.lrelu(x)
encoded_state = self.output(x)
return encoded_state
Source Distribution, w(a|s)
class source_distribution(nn.Module):
def __init__(self,
action_space,
conv_kernel_size,
conv_layers,
hidden, input_channels,
height, width,
state_space=None,
use_encoded_state=True):
super(source_distribution, self).__init__()
self.state_space = state_space
self.action_space = action_space
self.hidden = hidden
self.input_channels = input_channels
self.conv_kernel_size = conv_kernel_size
self.conv_layers = conv_layers
self.height = height
self.width = width
self.use_encoding = use_encoded_state
# Source Architecture
# Given a state, this network predicts the action
if use_encoded_state:
self.layer1 = nn.Linear(in_features=self.state_space, out_features=self.hidden)
self.layer2 = nn.Linear(in_features=self.hidden, out_features=self.hidden)
self.layer3 = nn.Linear(in_features=self.hidden, out_features=self.hidden*2)
self.layer4 = nn.Linear(in_features=self.hidden*2, out_features=self.hidden*2)
self.hidden_1 = nn.Linear(in_features=self.hidden*2, out_features=self.hidden)
else:
self.layer1 = nn.Conv2d(in_channels=self.input_channels,
out_channels=self.conv_layers,
kernel_size=self.conv_kernel_size, stride=2)
self.layer2 = nn.Conv2d(in_channels=self.conv_layers,
out_channels=self.conv_layers,
kernel_size=self.conv_kernel_size, stride=2)
self.layer3 = nn.Conv2d(in_channels=self.conv_layers,
out_channels=self.conv_layers*2,
kernel_size=self.conv_kernel_size, stride=2)
self.layer4 = nn.Conv2d(in_channels=self.conv_layers*2,
out_channels=self.conv_layers*2,
kernel_size=self.conv_kernel_size, stride=2)
self.hidden_1 = nn.Linear(in_features=self.height // 16 * self.width // 16 * self.conv_layers * 2,
out_features=self.hidden)
# Leaky relu activation
self.lrelu = nn.LeakyReLU(inplace=True)
# Hidden Layers
self.output = nn.Linear(in_features=self.hidden, out_features=self.action_space)
# Output activation function
self.output_activ = nn.Softmax()
def forward(self, current_state):
x = self.layer1(current_state)
x = self.lrelu(x)
x = self.layer2(x)
x = self.lrelu(x)
x = self.layer3(x)
x = self.lrelu(x)
x = self.layer4(x)
x = self.lrelu(x)
if not self.use_encoding:
x = x.view((-1, self.height//16*self.width//16*self.conv_layers*2))
x = self.hidden_1(x)
x = self.lrelu(x)
x = self.output(x)
output = self.output_activ(x)
return output
Inverse Dynamics Distribution, q(a|s’, s)
class inverse_dynamics_distribution(nn.Module):
def __init__(self, state_space,
action_space,
height, width,
conv_kernel_size,
conv_layers, hidden,
use_encoding=True):
super(inverse_dynamics_distribution, self).__init__()
self.state_space = state_space
self.action_space = action_space
self.height = height
self.width = width
self.conv_kernel_size = conv_kernel_size
self.hidden = hidden
self.conv_layers = conv_layers
self.use_encoding = use_encoding
# Inverse Dynamics Architecture
# Given the current state and the next state, this network predicts the action
self.layer1 = nn.Linear(in_features=self.state_space*2, out_features=self.hidden)
self.layer2 = nn.Linear(in_features=self.hidden, out_features=self.hidden)
self.layer3 = nn.Linear(in_features=self.hidden, out_features=self.hidden * 2)
self.layer4 = nn.Linear(in_features=self.hidden * 2, out_features=self.hidden * 2)
self.hidden_1 = nn.Linear(in_features=self.hidden * 2, out_features=self.hidden)
self.conv1 = nn.Conv2d(in_channels=self.input_channels*2,
out_channels=self.conv_layers,
kernel_size=self.conv_kernel_size, stride=2)
self.conv2 = nn.Conv2d(in_channels=self.conv_layers,
out_channels=self.conv_layers,
kernel_size=self.conv_kernel_size, stride=2)
self.conv3 = nn.Conv2d(in_channels=self.conv_layers,
out_channels=self.conv_layers * 2,
kernel_size=self.conv_kernel_size, stride=2)
self.conv4 = nn.Conv2d(in_channels=self.conv_layers * 2,
out_channels=self.conv_layers * 2,
kernel_size=self.conv_kernel_size, stride=2)
# Leaky relu activation
self.lrelu = nn.LeakyReLU(inplace=True)
# Hidden Layers
self.hidden_1 = nn.Linear(in_features=self.height // 16 * self.width // 16 * self.conv_layers * 2,
out_features=self.hidden)
self.output = nn.Linear(in_features=self.hidden, out_features=self.action_space)
# Output activation function
self.output_activ = nn.Softmax()
def forward(self, current_state, next_state):
state = torch.cat([current_state, next_state], dim=-1)
if self.use_encoding:
x = self.layer1(state)
x = self.lrelu(x)
x = self.layer2(x)
x = self.lrelu(x)
x = self.layer3(x)
x = self.lrelu(x)
x = self.layer4(x)
x = self.lrelu(x)
x = self.hidden_1(x)
else:
x = self.conv1(state)
x = self.lrelu(x)
x = self.conv2(x)
x = self.lrelu(x)
x = self.conv3(x)
x = self.lrelu(x)
x = self.conv4(x)
x = self.lrelu(x)
x = x.view((-1, self.height // 16 * self.width // 16 * self.conv_layers * 2))
x = self.hidden_1(x)
x = self.lrelu(x)
x = self.output(x)
output = self.output_activ(x)
return output
Problems
- The above training approach is complex and does not really perform well in discrete action space environments such as the hard exploration game, Montezuma’s Revenge.
- My aim going forward to have a simple, scalable (using SGD) and efficient method to have an intrinsically motivated agent, similar to what was achieved in Curiosity driven exploration.
Empowerment for discrete action spaces. (Current Research)
For the past few months, I have been dabbling with intrinsic rewards for the atari games. Learning these games and reaching super human performance is non trivial, especially for sparse reward games such as Montezuma’s revenge, where exploration is of prime importance. Lately, there has been work on agents that are trained only using intrinsic rewards and no external rewards (Curiosity is all you need) but there are other forms of intrinsic motivations that can be used, namely Empowerment.
Now, I will explain the model that would enable an agent to learn in atari games using empowerment (with or without extrinsic rewards).
How to calculate Mutual Information with standard, simple SGD ?
Using Mutual Information Neural Estimation. What is that ?
MINE is a simply uses the dual representation of the mutual information KL representation to get an easy formulation of the mutual information to maximize or minimize or estimate.
Recall the mutual information KL representation-
Now, there is a thing called the dual representation of the KL divergence. The paper primarily works with the Donsker-Varadhan representation of the KL divergence.
What is the Donsker-Varadhan Representation?
The KL divergence admits the following dual representation :
For the proof, I refer you to the paper - Mutual Information Neural Estimation. (It is pretty straightforward).
We can then choose a family of functions F T: X x Z -> R parameterized by a deep neural network. And that is it. Really simple and elegant.
The Algorithm then.
Suppose you have 2 random variables, X and Z.
- Initialize the network parameters.
- Draw a minibatch of samples from the joint distribution. This means the batch would consist of (x, z) samples.
- By simply dropping x or z from the samples, we can get the respective marginals.
- Use the above representation to estimate a lower bound to the Mutual Information.
- Evaluate the gradient.
- Do an gradient ascent step.
- Repeat until convergence.
How can we use this for Reinforcement Learning ?
Recall empowerment was the mutual information between the action and the subsequent state that was reached due to that action. Calculating the mutual information using the aforementioned method is a bit of a pain. What if we could use the simple formulation given by MINE.
Then, empowerment could be represented by MINE in the following manner
Again, we run into the problem of p(s’|s) which is intractable for continuos action spaces but since we are dealing with discrete action spaces, we can easily sum over all actions.
How do we get the samples from the joint?
For the joint distribution p(s’, a|s), the samples from the replay buffer can be used. (Note that the replay buffer is filled by executing the actions from the policy distribution, w).
Therefore the samples for the first half of the Mutual Information equation are the s’ and a of the tuples (s, a, s’).
How do we get the samples from the marginal distributions ?
For the marginal distribution p(s’|s), we take the current state and sample all possible actions (possible due to the discrete action space assumption)and give these as input to the forward dynamics model (f(s’|s, a)) and then average out the result to get the s’ for the corresponding s.
For the marginal distribution w(a|s), we just sample from the minibatch. Thus, we get the a and s required for the second term.
What next ?
After having calculated the joint and marginal distributions, we can then sample from these to calculate the lower bound to the mutual information (a.k.a the empowerment of the state).
We have the empowerment. What now?
The empowerment calculated can now be directly utilized as an intrinsic reward for any policy learning algorithm. Here, I would be using Deep Q Learning.
The Algorithm.
- Initialize a forward model f(s, a) and policy w.
- Initialize the environment
- Sample actions from policy distribution w(a|s) (Using a random exploration policy, intially) and execute the actions.
- Store the resulting tuples (s, a, s’, r_e) in the replay buffer.
- Sample a batch of tuples from the replay buffer.
- Train the forward model.
- Sample the joint and the marginal distributions as mentioned above and calculate the mutual information.
- Gradient ascent on the statistics network, T.
- Store the mutual information as a reward, r_e + beta*mutual_information, in the replay buffer.
- Train the DQN Network.
- Repeat until convergence.
Statistics Network
class StatisticsNetwork(nn.Module):
def __init__(self, state_space,
action_space,
hidden, output_dim):
super(StatisticsNetwork, self).__init__()
self.state_space = state_space
self.action_space = action_space
self.hidden = hidden
self.output_dim = output_dim
# Statistics Network Architecture
self.layer1 = nn.Linear(in_features=self.state_space+self.action_space,
out_features=self.hidden)
self.layer2 = nn.Linear(in_features=self.hidden, out_features=self.hidden)
self.output = nn.Linear(in_features=self.hidden, out_features=self.output_dim)
# Leaky Relu activation
self.lrelu = nn.LeakyReLU(inplace=True)
# Initialize the weights using xavier initialization
nn.init.xavier_uniform_(self.layer1.weight)
nn.init.xavier_uniform_(self.layer2.weight)
nn.init.xavier_uniform_(self.output.weight)
def forward(self, next_state, action):
s = torch.cat([next_state, action], dim=-1)
x = self.layer1(s)
x = self.lrelu(x)
x = self.layer2(x)
x = self.lrelu(x)
output = self.output(x)
return output
Policy Training
for frame_idx in range(1, self.num_frames+1):
epsilon_by_frame = epsilon_greedy_exploration()
epsilon = epsilon_by_frame(frame_idx)
action = self.policy_network.act(state, epsilon)
# Execute the action
next_state, reward, done, success = self.env.step(action.item())
episode_reward += reward
if self.clip_rewards:
reward = np.sign(reward)
next_state = to_tensor(next_state, use_cuda=self.use_cuda)
with torch.no_grad():
next_state = self.encoder(next_state)
reward = torch.tensor([reward], dtype=torch.float)
done_bool = done * 1
done_bool = torch.tensor([done_bool], dtype=torch.float)
# Store in the replay buffer
self.store_transition(state=state, new_state=next_state,
action=action, done=done_bool,reward=reward)
state = next_state
if done:
epoch_episode_rewards.append(episode_reward)
# Add episode reward to tensorboard
episode_reward = 0
state = self.env.reset()
state = to_tensor(state, use_cuda=self.use_cuda)
state = self.encoder(state)
# Train the forward dynamics model
if len(self.replay_buffer) > self.fwd_limit:
# Sample a minibatch from the replay buffer
transitions = self.replay_buffer.sample_batch(self.batch_size)
batch = Buffer.Transition(*zip(*transitions))
batch = self.get_train_variables(batch)
mse_loss = self.train_forward_dynamics(batch=batch)
stats_loss, aug_rewards, lower_bound = self.train_statistics_network(batch=batch)
if self.clip_augmented_rewards:
# Clip the augmented rewards.
aug_rewards = torch.sign(aug_rewards)
policy_loss = self.train_policy(batch=batch, rewards=aug_rewards)
if frame_idx % self.print_every == 0:
print('Forward Dynamics Loss :', mse_loss.item())
print('Statistics Network loss', stats_loss.item())
print('Policy Loss: ', policy_loss.item())
Experiments
The models were trained and executed on the hard exploration game of Montezuma’s Revenge. The following hyperparameters were used without any hyperparamater search.
Batch Size: 64 Environment Embedding Size: 64 Hidden Size (For all networks): 64 Intrinsic Parameter beta: 0.1
Results
Without any intrinsic rewards and just using the external reward signal of the game, standard DQN fails to achieve any rewards whatsover. However, after using the empowerment values as intrinsic rewards, the agent is consistently able to achieve rewards and is also able to exit the first room.
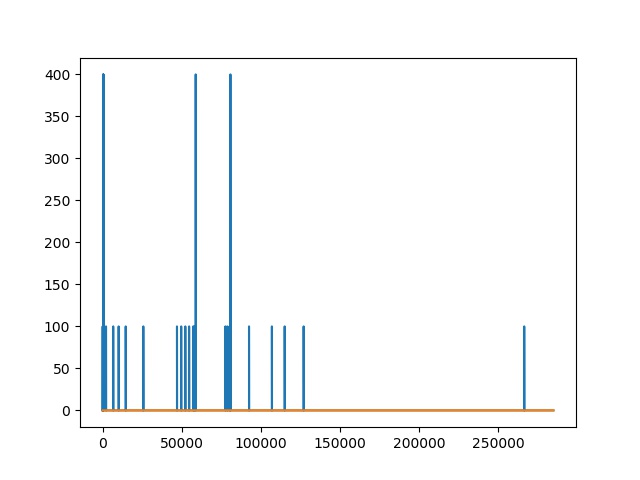
The orange color represents the agent without intrinsic rewards and the one with the blue color represents the empowerment driven agent.
Some Insights
- During the initial training, I was using the standard KL divergence form of the mutual information as demonstrated in Belghazi et al. however, since KL is not bounded this made the training unstable. Simply switching the KL with Jensen Shannon divergence greatly improved training stability.
- Reward scaling was really important to avoid situations where the Q network diverged.
- Slow training (lower learning rate) for the statistics network also helped improve stability.
Future Direction
The results achieved show the validity of the method but I believe that given better computational resources, this method could possibly be used as an unsupervised control mechanism. Currently, the main factor limiting the performance is, I believe, the environment embedding size which is using random features. A size of 64 may be insufficient for atari and we may have to use atleast an embedding size of 512 (Similar to Large Scale study of Curiosity).
Inspiration from recent papers
Following the results from Exploration by random distillation, the following methods could also be implemented for better results:
- Using only intrinsic rewards and treating the problem as non-episodic.
- Using 2 value heads for the intrinsic and extrinsic rewards resepectively.
- High discount factor for the external rewards (Anticipate rewards well into the future).
- Use sticky actions to avoid relying on the game’s determinism.
- Normalize the intrinsic reward.
- Observation normalization is essential too.
You could find the code in the following github repository and feel free to tinker.
The Complete Research Paper
Empowerment driven Exploration using Mutual Information Estimation
My Paper (mentioned above) got accepted at Bayesian Deep Learning Workshop, NIPS 2018. Thank all for the valuable feedback.
Tensorflow implementation (Under development)
I have made a number of key changes to the original architecture and algorithm in lieu of better results on Atari. Wish me luck !
Github Repository
Unsupervised Real-time control through Variational Empowerment
Variational Information Maximisation for Intrinsically Motivated Reinforcement Learning